例題14-2:データを操作する¶
A: さて、というわけで例題14-1の続きでもうちょっと複雑なデータ操作をしよう。例題14-1を飛ばした読者の皆さんは 14-1.zip をダウンロードしておいてください。
B: ちょ、Aさん、なにが「というわけで」なんですか。唐突すぎます。
A: ふっ…、実はな、作者のアホが例題14-2の原稿を結構な分量書き進めたんだがな、うっかりセーブする前にエディタを閉じちまったんだな…。
B: あー。相変わらずアホですねえ。
A: で、もう作者が書き直す気力を失っちゃったんで、こういう出だしになったわけだ。やれやれ。
B: ホント、やれやれですねえ。
A: さて、これが今回のサンプルプログラムその1なわけだが…
B: あ、本題に入る前にちょっと気になったんですが。
A: 何?
B: 今回のタイトル「データを操作する」ってなんだか データの捏造みたい で微妙ですよねえ。
A: …言いたいことはそれだけか。
B: そんな冷たい目でみないでくださいよ。責めるならぼくにこんなつまらないことを言わせる作者を責めてください。
A: 本当にどうしようもない作者だよなあ。
B: 本当にねえ。
1import os
2import os.path
3import pylab
4
5cndList = ['E1-MRot','E2-MRot','E3-MRot','E4-MRot','E5-MRot','E6-MRot']
6nCnd = len(cndList)
7nPB = 2
8nDir = 4
9
10L = 0
11R = 1
12NA = 2
13B = 0
14P = 1
15
16reactionTimePB = []
17reactionTimeDir = []
18reactionTimeLRPBDir = []
19
20for (root, dirs, files) in os.walk(os.getcwdu()):
21 if root == os.getcwdu():
22 continue
23 tmpReactionTimePB = [0 for i in range(nCnd*nPB)]
24 tmpReactionTimeDir = [0 for i in range(nCnd*nDir)]
25 for f in files:
26 r,e = os.path.splitext(f)
27 if e.lower() == '.txt':
28 fp = open(os.path.join(root,f),'r')
29 line = fp.readline()
30 for i in range(nCnd):
31 if line.find(cndList[i])>=0:
32 cndidx = i
33 break
34
35 tmpData = pylab.zeros((96,5))
36 idx = 0
37 for line in fp:
38 data = line.rstrip().split(',')
39 if data[0]=='L':
40 tmpData[idx,0] = L
41 else:
42 tmpData[idx,0] = R
43 if data[1]=='B':
44 tmpData[idx,1] = B
45 else:
46 tmpData[idx,1] = P
47 tmpData[idx,2] = int(data[2])
48 tmpData[idx,3] = float(data[3])
49 if data[4]=='L':
50 tmpData[idx,4] = L
51 elif data[4]=='R':
52 tmpData[idx,4] = R
53 else:
54 tmpData[idx,4] = NA
55
56 idx += 1
57
58 fp.close()
59
60 correct = tmpData[:,0]==tmpData[:,4]
61 tmpReactionTimePB[cndidx] = pylab.mean(tmpData[correct & (tmpData[:,1]==B),3])
62 tmpReactionTimePB[nCnd+cndidx] = pylab.mean(tmpData[correct & (tmpData[:,1]==P),3])
63
64 for i in range(nDir):
65 d = i*90
66 tmpReactionTimeDir[nCnd*i+cndidx] = pylab.mean(tmpData[correct & (tmpData[:,2]==d),3])
67
68
69
70 reactionTimePB.append(tmpReactionTimePB)
71 reactionTimeDir.append(tmpReactionTimeDir)
72
73reactionTimePB = pylab.array(reactionTimePB)
74pylab.figure()
75pylab.errorbar(pylab.arange(nCnd),pylab.mean(reactionTimePB[:,:nCnd],0),yerr=pylab.std(reactionTimePB[:,:nCnd],0,ddof=1),fmt='o-',label='Back')
76pylab.errorbar(pylab.arange(nCnd)+0.05,pylab.mean(reactionTimePB[:,nCnd:],0),yerr=pylab.std(reactionTimePB[:,nCnd:],0,ddof=1),fmt='o-',label='Palm')
77pylab.xticks(pylab.arange(nCnd),cndList,rotation=22.5)
78pylab.legend()
79
80reactionTimeDir = pylab.array(reactionTimeDir)
81pylab.figure()
82for i in range(nDir):
83 pylab.errorbar(pylab.arange(nCnd)+0.05*i,pylab.mean(reactionTimeDir[:,i*nCnd:(i+1)*nCnd],0),yerr=pylab.std(reactionTimeDir[:,i*nCnd:(i+1)*nCnd],0,ddof=1),fmt='o-',label=str(i*90)+'deg')
84pylab.xticks(pylab.arange(nCnd),cndList,rotation=22.5)
85pylab.legend()
86
87pylab.show()
B: アホみたいな導入だった割にはいきなり難しそうなプログラムですね。
A: 58行目までは例題14-1とほとんど同じだよ。
B: いや、その後が難しそうなんですが…。
A: ふむ。全然難しくないんだがな…と言いたいところだが、正直この手のデータ処理プログラムは読みにくい。他人が書いたものは特にそうだ。いろいろな理由があるだろうが、多分ひとつは最終的にどのような形にデータを整理しようとしているかがわかりにくいから。 ゴールがわからないと「なぜ今ここでこの処理をしなければいけないのか?」がわかりにくい。
B: ふむふむ。なんだか模型と似てる気がする。
A: そして、何度も繰り返し言っているがfor i in range(5):とかって書いてあって「5って何の値?」ってパターンだな。書いている本人は良くても、後から読まされる人にとっては「5とは何の値か当てなさい」ってなクイズみたいなもんだ。
B: そう何度も繰り返し言ってる本人が例題14-1ではpylab.arange(6)とか書いてたくせに。
A: ふっ、そうくると思ってな、6行目から8行目のように各要因の水準数を変数に代入しておいた。例題14-1で「6」と生の値を入れていたところは全部書き直してある。
B: 威張りたいんなら最初からそうしとけばいいのに。
A: ほっとけ。で、この14-2a.pyでは以下のようなグラフの描画を目指す。そのために、グラフの下のようにデータを並べる。
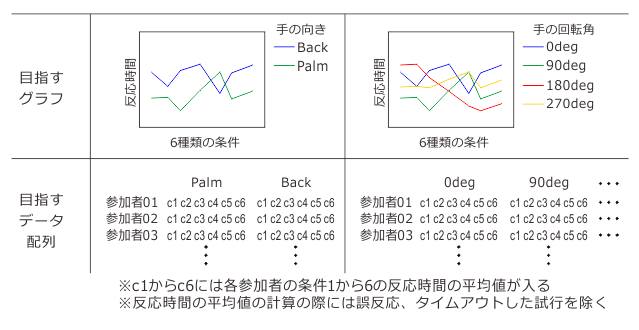
B: なんだかExcelでグラフ作る時みたいでわかりやすいです。でもExcelの並べ方とちょっと違うな、Excelでこんなグラフ描くなら列方向は実験条件でいいけど行方向はBackかPalmじゃないといけないような。
A: 本来なら例題14-1でもこういう図を載せとくべきだったんだがな。やる気が出なかったもんで。Excelと並び方が違うというのはまあその通りなんだが、このデータ配置は参加者全員の平均を計算する前段階のものだ。最終的には…
B: Excelと同じ形になるんですか?
A: いや、ならない。
B: (ガクッ)
A: そうする必要ないんだ。この図に示したデータ配置から直接全参加者の平均値と標準偏差を計算して目的のグラフをプロットすることができる。もちろんExcelと同じように並べてグラフを描くこともできるが、Excelと同じようにするくらいなら最初からExcelで描いた方がいい。
B: おお、なんだかもっともらしいことを言われている気がする。
A: さて、23行目と24行目では、参加者ごとの平均を格納しておくためのリストを用意している。Palm/Backの方はnCnd(=6)条件×nPB(=2)条件の値を納めないといけないから長さnCnd * nPBのリスト、回転角の方はnCnd(=6)条件×nDir(=4)4条件で長さnCnd * nDirのリストを確保している。
B: リストの内包表記( 例題3-3 )ですね。さすがに覚えたぞ。
A: で、60から66行目が前半の難関だが…。どうしよう。プログラムの順番通りに解説するか。ここで目指すことは以下の通り。
正答している試行を抜き出す。
正答していて、なおかつ平均を計算しようとしている条件の試行を抜き出す。
抜き出した試行における反応時間の平均を求める。
B: ふむふむ。
A: まず正答している試行の抜き出し。これは例題14-1で誤答率を求めた時の逆だからそんなに難しくないだろう。tmpData[:,0] == tmpData[:,4]とすれば、tmpDataの0列目と4列目の値が等しい試行はTrue、等しくない試行はFalseのベクトルが得られる。これは後で利用するのでとりあえずcorrectという変数に格納しておく。
B: 0列目は刺激が右手か左手か、4列目は参加者の反応でしたね。
A: そう。続いて61行目と62行目だが、これはわかるか?
B: ええと、これは…。ややこしいな。
A: ややこしいときは内側のカッコから外側へ向かって読むんだ。
B: 一番内側は…、tmpData[:,1]==Bか。tmpDataの1列目がBの行を抜き出してるんですね。
A: そう。こういう所でで刺激のBack/Palmを示す数値をBやPという名前の変数に格納していたご利益が出てくる。もしそういう工夫をしていなければ、Backに0を割り当てていたんだから(13行目)ここはtmpData[:,1]==0と書く破目になっていたはず。そうすると後から読むときに「1列目ってなんだったけ、0って何を指してるんだっけ?」と考えなきゃいけない。
B: でもBって書いてあっても「Bってなんだったっけ?」てなりそうな気がしますが。ぼくなら半年もしたらそうなる自信があります。
A: そんなこと自信満々に言うな。まあ、確かにB君の言うとおり、Bという表記でも忘れるときは忘れる。かといってもっと詳しい名前を付けるとプログラムを書くときに鬱陶しい。結局、どこかで妥協できるポイントをさがさなければならない。 で、次はtmpData[:,1]==Bと先ほど保存したcorrectの&、すなわち論理積をとっている。論理積ってなんだったか覚えてるか?
B: もちろん。両方とも真なら真、それ以外は偽。
A: よろしい。tmpData[:,1]==Bとcorrectの論理積をとることによって、刺激がBackかつ正答した試行だけがTrueとなるベクトルが得られる。そうそう、演算子の優先順位の関係で tmpData[:,1]==Bは( )でくくっておかないと怒られるから注意するように 。Matlabから移った人はここで躓くことがあるので注意が必要だ。
B: …Aさん自身が躓いたんだろうな
A: 反応時間は3列目に格納してあるんだからtmpData[correct & (tmpData[:,1]==B), 3]とすれば該当する試行の反応時間が格納されたベクトルが得られる。これをpylab.mean()に渡せば反応時間が得られるというわけだ。
B: うーん。難しい。
A: まあ慣れていないと難しいかも知れんが、この操作自体は例題12-2とかですでに取り上げたことがある。ここからが今回の例題14-2で取り上げたい操作だ。61行目、62行目の左辺の意味はわかるか?
B: 左辺? 計算した平均をtmpReactionTimePBに保存しているんですよね?
A: 問題は保存するリスト上の位置だ。なぜ刺激がBackの試行はtmpReactionTimePB[cndidx]、Palmの試行はtmpReactionTimePB[nCnd+cndidx]になるかわかるか?
B: えぇっ、えっと…
A: 目標とするデータ配置を思い浮かべて落ち着いて考えてごらん。cndidxには6種類の条件を指し示す0から5のいずれかの値が入っている。 で、tmpReactionTimePBの0から5番目にBack試行の平均値を保存するんだから、Back試行は普通にtmpReactionTimePB[cndidx]に保存すればいい。 一方、Palm試行の平均値はtmpReactionTimePBの6から11番目に保存するわけだが、cndidxに条件数である6を加えるとうまい具合に6から11の値が得られるんだ。 だから、Palm試行の平均値はtmpReactionTimePB[nCnd+cndidx]に保存すればいいということになる。

B: こうやって図にしてみるとよくわかりますね。
A: プログラムを書いていて自分でも訳がわからなくなってきたら、こういう図を描いてみるといいよ。 で、この考え方を一般化したのが次の刺激回転角別の平均値の計算をする64から66行目だ。
B: 一般化?
A: そう。Palm/Back別の平均の計算では刺激の種類が2種類しかなかったから61行目、62行目のように1行ずつ書いてもそんなに手間じゃないが、もし刺激の種類が12種類あったらどうする。1行ずつ書いてたら面倒臭いだろ。面倒臭いだけならいいが、書き間違えたらその後のデータ分析がすべてパァになる。
B: 間違えても実行してみたらすぐにわかるんじゃないんですか?
A: 3秒以内に反応した試行しか含んでないはずなのに平均を計算したら152秒になったとかいった具合に、明らかにおかしな値が出てきたらわかるだろうな。 けれども、だいたい700ミリ秒前後になるだろうと予想していて、正しい計算結果は1200ミリ秒なのにプログラムが間違っていて750ミリ秒とかいう値が出てきたら? 一番怖いのは「あ、だいたい予想通りの結果が出てるな、よしよし」と受け取ってしまって、間違えたまま発表してしまうことだ。 B君が言うとおり、計算結果の数値がおかしくて計算間違いに気づくことも多い。しかし、それだけに頼ってはいけないんだよ。
B: …なんか急にAさんがまじめになったんでびっくりしました。
A: 最初からずっとまじめだっつうの。さて、そんなわけで、リスト上の計算結果を格納すべき位置に規則性があるのなら、その規則に従ってプログラムで位置を決定した方がいい。 さっきのBack/Palm別の平均値の計算と同じように、刺激の回転角別の平均値を計算することを考えよう。この場合、実験条件は6種類で同じだが、刺激の種類が0度、90度、180度、270度の4種類ある。 これまたさっきのBack/Palm別の平均値の計算と同じように、計算結果を格納すべきリスト上の位置を図にしてみるとこうなる。
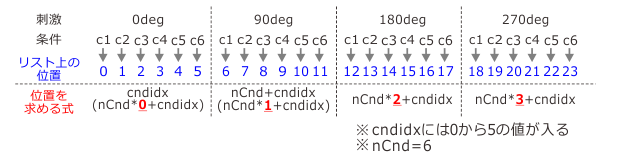
B: ちょっと字が小さくて見難いですね。
A: 省略せずに押し込んだからな。我慢してくれ。で、今回は刺激4種類×6条件で長さ24のリストにデータを格納してくわけだが、注目してほしいのは一番下の「位置を求める式」という行だ。4種類の刺激を0から3の値で示すとする。Back/Palm別の例では最初の刺激(Back)についてはcndidx、第二の刺激(Palm)についてはnCnd+cndidxでリスト上の位置を求められたわけだが、これらはそれぞれ nCnd*0 +cndidx、 nCnd*1 +cndidxと書くことができる。 そして、同様に、第三の刺激については nCnd*2 +cndidx、第四の刺激については nCnd*3 +cndidxと書けることを確認してほしい。
B: おお、確かに確かに。
A: ということは、適当な変数、例えばiを使ってforループを組んで、その中でtmpReactionTimeDir[ nCnd*i +cndidx]へ平均の計算結果を代入すれば、平均を計算する式自体は1行だけ書けばよい。 それがまさに64から66行目のforループなわけだ。ちょっと65行目のd=90*iがエレガントじゃないがな。
B: ええっと、この65行目は…、あ、平均を計算する刺激の回転角を求めているのか。
A: 今回は偶然、刺激の種類が等差数列で表せる数値(0,90,180,270)で表現されているからな。こういう手が使える。そうじゃない場合は5行目のcndListのようなものを準備する必要があるだろう。これは次の例題14-3で実例を出してみるかな?
B: えー。行き当たりばったりのAさんがそんな予告しちゃっていいんですか?
A: 実はもう例題14-3のスクリプトは用意してある。正確に言うと、今回扱うつもりだったんだが予定より今回が長くなってしまいそうなんで後半は分割して例題14-3とする予定だ。
B: ぐは、じゃあ今回はまだ続くんですか。
A: うむ。覚悟するように。64から66行めの書き方は非常に応用範囲が広いからマスターしておくといいぞ。
B: へーい。
A: さて、あるディレクトリに含まれるすべての拡張子が.txtのファイルに対して25行目から66行目までの処理が完了したら、tmpReactionTimePBとtmpReactionTimeDirのすべての要素に計算結果が代入されている。これらが参加者1人分のデータに相当する。で、これらのデータを全参加者のデータを格納するためのリストreactionTimePBとreactionTimeDirにappendする。70行目と71行目だな。まだ処理していないディレクトリがあったら、tmpReactionTimePBとtmpReactionTimeDirは次の参加者のデータを格納するために初期化されて再利用される。1人分の処理が終わったら使い捨て、というつもりでtmpほげほげという変数名にしているが、これは単なる私の趣味。
B: それは趣味の問題なんですか? 変な趣味。
A: なんだその突っ込みは。趣味という言い方がアレなら習慣でもなんでもいい。 すべての参加者に対する処理が終了したら、いよいよ73行目以降のグラフ描画に突入する。
B: やっとですか。長かったですね…。
A: まず73行目はpylab.array()を使ってreactionTimePBをnumpy.ndarray型に変換している。例題14-1でもちょっと言ったけど、こんな手順を踏んでいるのは後から参加者を追加したときにプログラムを書き変えなくても対応できるようにするため。もう今以上参加者が増えないことがはっきりしているのなら参加者数と同じ行数を持つnumpy.ndarray型の変数を用意してもいい。初心者を卒業した人のために言っておくと、numpy.ndarray型でもpylab.vstack()という関数を使うと行をどんどん追加していくことができるので、リストを使わずにそっちでやってもいい。詳しくはhelp pylab.vstackで。
B: 次々といろんな話が出てきて混乱してきました。
A: ん。今回の例題はあっさり済ませるつもりだったんだが、いざ解説を始めてみると結構言わないといけないことがあることに気付いた。自分でプログラムを書くときはこのあたりの事はなーんも考えずに書いてるんだな。例題14は全般的に今までこの手のデータ操作をするプログラムを書いたことがない人にはなかなか手ごわいかも知れない。そういう方は、今のnumpy.ndarrayの話とかは飛ばしてとにかくひとつの方法で慣れることを優先してほしい。
B: どこが飛ばしていい話なのかすらわからないんですが…
A: ぐっ、まあ、確かに重要じゃないかどうか判断できるくらいなら内容理解できるわな。B君に言い負かされてしまった。
B: 別にそんなつもりじゃないんで話を続けてください。わからなかったら聞きますんで。
A: ああ、じゃあ続けるか。えーっと、どこまで話したかというと…73行目までか。 74行目からいよいよグラフ描画だが、ここで未紹介の関数pylab.figure()というのが出ている。 これはグラフ描画のための新しいウィンドウを開く関数で、複数のグラフを描画したいときに便利だ。あともうひとつpylab.subplot()というのもあるが、これは例題14-3で説明する。
B: subplot()てのは例題14-1で見ましたが。Aさんが疲れたとか言って説明放棄してましたが。
A: え、そ、そうだっけ。そりゃ失礼。pylab.figure()の引数や戻り値をうまく利用すると複数のグラフをマネージできるんだが、それをここで説明しだすとややこしくなるんでここではやめておこう。開いたウィンドウはpylab.close()すれば閉じる。 続いて75行目のpylab.errorbar。
B: ついに来た。さすがに今回は解説するんでしょうね?
A: そんな怖い目で見るなよ。さすがに今回はちょっと解説しておくか。pylab.errorbar()はpylab.plot()と同じように第1引数プロットする折れ線のX軸の値、第2引数にY軸の値を指定する。で、xerr、yerrという引数でエラーバーの長さを指定できる。もちろんxerrは横方向、yerrは縦方向のエラーバーね。
B: エラーバーってたいてい縦に引いてあると思うんですけど、横にも引くんですか?
A: 横向きの棒グラフとかだったら普通に横向きにエラーバー引くだろ。それに、2次元のデータについてそれぞれの次元の標準偏差を同時に示したい場合は縦と横のエラーバーを同時に描くこともある。
B: あ、そういえばそういうグラフ見たことあるような気がします。
A: 当然、第1引数と第2引数の要素数は一致していなといけないし、xerrやyerrを指定する場合はそれらの要素数も一致していなければいけない。ひとつ注意したいのは、グラフの色や線といった書式指定した場合だ。
B: pylab.plot()と同じじゃないんですか?
A: いや、基本的に同じなんだが、pylab.plot()の場合は第2引数に続けて第3引数に線の書式を指定する文字列を書けばよかった。しかし、pylab.errorbar()では文法上の問題で、fmt='ほげほげ'といった具合に名前付きの引数として指定してやらないといけない。 このあたりは Matlabの同名の関数errorbar()と異なるので、Matlabから来た人は注意が必要だ 。
B: またMatlabの名前が。Aさんはずいぶん意識してますねえ。
A: やっぱり利用者が多いからな。就職したラボではMatlabを使わなきゃいけない、ってこともあるだろうし。いずれMatlab←→pythonの注意点なんかも扱いたいな。
B: 相変わらず夢だけはどんどん広がってますね。
A: ほっとけ。75行目では第1引数にpylab.arange(nCnd)を指定している。pylab.range()は例題2とかでも登場しているんだが、range()のように等差数列を作る関数だ。range()と違うのは少数の増分を持つ数列を作れることと、戻り値がリストではなくnumpy.ndarrayであること。ここでは条件数が格納されているnCndを引数に指定している。続いて第2引数だが、ここはreactionTimePBでPalm刺激に対する結果に相当する0列目から5列目を抜き出して列ごとの平均を計算している。ここがわからない人は 例題12-2 とこの図を見ながらよーーーーーーーーーーーーーっっく復習してほしい。

B: えらい力入ってますね。
A: 毎回説明していたらキリがないからな。続いてyerrの引数を計算しているが、これは平均が標準偏差になっただけなので第2引数がわかれば問題ないでしょ。 例題12-2 を復習してくださいませませ。で、最後にfmtで書式指定。ここでは色を指定せずpython任せにして、実線で結んで・を打ってねってことだけ指定。
B: 色を指定しなかったら勝手に決めてくれるんですか。
A: そう。楽でしょ。続く76行目は、75行目でreactionTimePBの0から5列目について計算していたのを6列目から11列目について計算しなおしただけ。以上。
B: 75行目を理解できるかがカギですね。
A: そうだな。で、出力はこの通り。
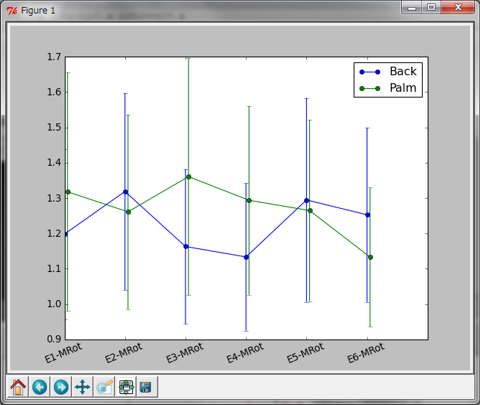
A: そうそう、ひとつ大事なことを言っておくと、 pylab.plotやpylab.errorbarといったグラフ描画関数を続けて実行すると、すでに描かれているグラフに重ねて描画される 。 Matlabな人は、何も指定しなければhold onの状態になっていると思っておけばいい 。 すでに描かれているグラフを消したい場合はpylab.clf()を使う といい。ちなみにMatlabで言うところのhold on/offを制御したい場合は、pylab.hold()を使うかholdという引数にTrue/Falseを指定する。
B: …これはMatlabな人以外は無視していい情報ですね?
A: ん。無視していいとは言わんが、初級を卒業した人向けの情報ではあるな。よくわからない人はパスしてください。
B: はーい。
A: 80行目からは刺激の回転方向別のグラフをプロットしている。先ほど61行目から66行目を解説した時と同じように、75行目、76行目の2行でほとんど同じような処理をしているのをfor文にまとめて、何種類刺激があっても同じforループで対応できるように書き直している。75行目の処理と下の図を見ながら、この82から83行目のforループを理解してほしい。この文が理解できれば、今回の例題は理解できたと自信をもっていい。

B: よし、ちょっとがんばるぞ。
A: B君ががんばっている間、読者の皆さんは出力のグラフをご覧ください。これ、メンタルローテーションの実験なんですが、正直あまりいいグラフじゃないですよね?
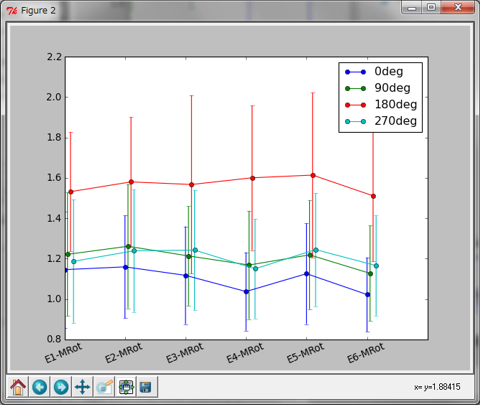
B: …なんだ、読んでみたら意外と簡単でした。僕も成長したかも。ところで、なんかさっきこのグラフがいいグラフじゃないとか何とかおっしゃってましたが。
A: うむ。B君もそう思わないか?
B: Aさんも自分でプログラム書いておいてそんな事言うんだから変人だよなあ。
A: これこそ教育的配慮と言ってほしいな。で、どう思う?
B: んー。これ、よく見るメンタルローテーションの反応時間のグラフじゃないですよねえ。メンタルローテーションのグラフって普通横軸に回転角が来ると思うんですけど。
A: その通り。このグラフでも180度の時に反応が遅いとかわからなくもないけど、ちょっと不親切だよな。
B: まあ、不親切と言われれば不親切ですねえ。
A: そこで、この14-2b.pyの登場となるわけだが…
B: なんだ、やたら誘導してくると思ったらちゃっかり準備していたわけですか。最初っからそっちを出してくれたらいいのに。
A: だから教育的配慮といっただろ。14-1a.pyで描いた2枚のグラフは基本的な考え方と、繰り返しをforループでまとめる解説のため。で、こっちの14-2b.pyは、 転んでもただでは起きない ことを示すため。
B: 転んでもただでは起きない?
A: そう。実験をする前からどういうグラフを描くか決まっている場合もあるが、データ処理の途中で「やっぱり横軸はこっちの方がいいんじゃないか?」と思うときもある。そういう時に、最初からプログラムを書き直すんじゃなくてすでにあるプログラムを再利用することを考える。
B: Aさんらしい発想ですね。なんでしたっけ、ズポラは美徳?
A: ズボラじゃなくて「怠惰」な。まあこの例自体はいわゆる「怠惰は美徳」とは異なるが。とにかく14-2b.pyを見てみよう。
行番号なしのソースファイル→ 14-2b.py ※IPython上で14-2a.pyを実行した後に続けて-iオプション付きで実行します。
1for i in range(nCnd):
2 idx = (pylab.arange(nCnd*nDir) % nCnd) == i
3 pylab.errorbar(pylab.arange(nDir)+0.02*i,pylab.mean(reactionTimeDir[:,idx],0),yerr=pylab.std(reactionTimeDir[:,idx],0,ddof=1),fmt='o-',label=cndList[i])
4pylab.xticks(pylab.arange(nDir),90*pylab.arange(nDir))
5pylab.legend()
6
7pylab.show()
B: な、なんだかずいぶん短いですね? 例題1-1より短いとは。
A: まずIPython上で14-2a.pyを実行しておいて、そのうえでこの14-2.pyを-i付きで実行してほしい。 つまり以下のようにするということだね。
In [2]: run 14-2a.py
In [3]: run -i 14-2b.py
B: この-iってなんですか?
A: IPythonの現在の名前空間で14-2b.pyを実行するということだ。 -iを付けずに実行すると14-2b.pyから14-2a.pyによって作成された変数の中身にアクセスすることはできないが、-iを付けるとあたかも14-2a.pyの最後に14-2b.pyを貼りつけて実行したかのように14-2a.pyで作成した変数にアクセスすることが出来る。
B: はあ、名前空間とかよくわかりませんが、おおよその意味はわかりました。
A: で、プログラムの内容だが、14-2a.pyと異なる処理をしているのは2行目だけだ。こっちの意味もわかるか?
B: ええっ、えっと。わからない時は内側の括弧から読む、でしたよね。
A: そうそう。
B: 一番内側はnCnd*nDir。実験条件と刺激の回転角の種類の掛け算。ということは、条件と回転角の組み合わせの個数。6×4で24。
A: そうそう、よしよし。
B: それがpylab.arange()の引数になっているんだから、0から23までの長さ24のベクトルができる。
A: うむ。
B: それで、nCndとの…。%ってなんでしたっけ。
A: 例題3-1 。 剰余 演算子だ。
B: 例題3-1が出てくるって珍しいですね。剰余ってなんでしたっけ。
A: a % bはaをbで割った時の余りだ。
B: そうそう、そうでした。ということは、2行目は0から23が格納されたベクトルを…? nCndで割った余り…? が、iに等しい???
A: やっぱりそこで詰まったか。この図を見ながらよく考えるといい。
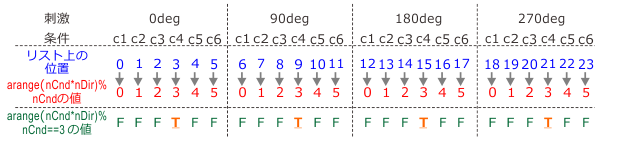
B: ええと、僕が今詰まったのは、%を使ってるところだから赤い数字のところですね。そうか、0から5の値が繰り返し出現するベクトルになるのか。これ、さっきreactionTimeDirを計算するときの処理の逆になるんですね!
A: その通り。 これはpythonではリストや行列の最初の要素を0番から数えるからこそ成立する計算だ。Matlabのように1から数える言語だと、わざわざ1を足すとか引くとかしなきゃいけないので面倒くさくてかなわん。
B: なんかえらく力が入ってますね。何事?
A: いや、ちょっといろいろ鬱積していてな。失礼。で、これがiと等しいという事は?
B: i番目の条件のデータが格納されている位置だけがTrueになる。
A: ご名答。図ではi=3の時の例を緑とオレンジで示しているが、3番目の条件、pythonでは0番目から数えるので図だとc4の条件に当たるわけだが、その位置でだけTrue、それ以外ではFalseとなるベクトルが得られることがわかる。 これをidxという変数に格納しておいて続く3行目で使っているわけだが、すでにここまで読み進めてきた皆さんならこれが何を意味しているかわかるはず。
B: すみません、わかんないです。
A: あらら。このまま気持ちよく終わるかと思ったが、ちょっと難しかったか。3行目のreactionTimeDir[:,idx]がどういう行列になるか想像できるか?
B: いや、それがわからないんですよ。
A: そうしたらIPythonで確かめてみよう。IPythonで14-2a.pyを実行した後、以下のように入力してみる。もちろん14-2b.pyを実行した後にやっても構わないので、すでに14-2b.pyを実行した人もIPythonを再起動する必要はない。iに代入するのは0から5の整数ならなんでもいいぞ。
In [12]: i = 3
In [13]: idx = (pylab.arange(nCnd*nDir) % nCnd) == i
In [14]: reactionTimeDir[:,idx]
Out[14]:
array([[ 1.27093083, 1.471902 , 1.43330479, 1.32303075],
[ 1.31537258, 1.53120205, 1.8460113 , 1.49725357],
[ 1.30802726, 1.39039388, 2.1594606 , 1.45690477],
[ 0.9028157 , 1.0658237 , 1.28936193, 0.98061922],
[ 1.08062917, 1.38520713, 1.66033575, 1.33653405],
(以下略)
B: 4列の行列だ。行数は…
A: こらこら、いちいち数えるな。IPythonを使ってるんだからpythonに数えてもらえ。
B: ええっ、どうするんでしたっけ。
A: len()を使ってもいいんだが、せっかくだからnumpy流に行くか。numpy.ndarrayはshapeという属性に行数や列数の値を持っている。こうすればいい。
In [15]: reactionTimeDir[:,idx].shape
Out[15]: (20, 4)
B: 20行4列ですね。
A: これでreactionTimeDir[:,idx]が何に対応しているかわかったか?
B: はいはい、えーっと、列方向に4種類の回転角、行方向に各参加者の形式でデータが格納された行列ですかね。
A: 「i番目の条件における」が抜けているが、まあ合格。この行列が得られれば、後は14-2a.pyの最後と同じだね。出力されるグラフは以下のとおり。
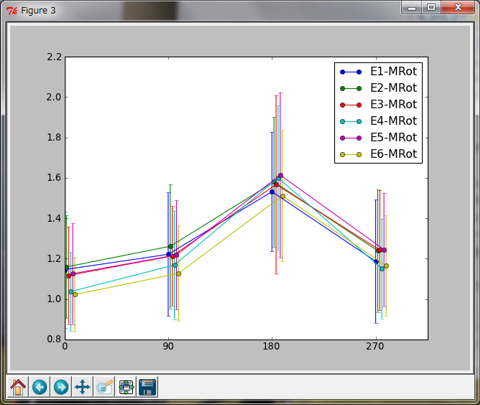
B: おおー。横軸が回転角のグラフだ。でも、苦労した割に実験条件の主効果とか回転角との交互作用とかなさそうなグラフですね。
A: それを言ってくれるなよ。とにかく、 剰余演算はこの手の処理で威力を発揮するのでぜひ覚えておいてほしい 。
B: へーい。
A: さて、以上で小手調べはおしまい。実は今回のデータの元の実験、「刺激が右手か左手か(2水準)」×「刺激が手の甲か手のひらか(2水準)」×「刺激の回転角(4水準)」×「実験条件(参加者の姿勢:6水準)」の4要因の実験計画なのね。横軸を回転角として、残りの要因の全ての組み合わせの折れ線グラフを描きたい。2×2×6=24本のグラフを描きたいってことだな。じゃあ、今回の応用としてB君にやってもらおうか。
B: ええっ、ちょっと待ってくださいよ…
------------------------------ 10分ほど経過 ------------------------------
B: だめです。ややこし過ぎてよくわかりません。2要因ならAさんのプログラムをちょっと書き直すだけですが、3要因となるとリスト上の位置の計算が…
A: だろうな。私がプログラムを書くんなら 絶対 今回と同じ方法ではやらないな。面倒くさくてかなわん。
B: えーっ、なんですかそれ、ひどい!
A: こういう処理は基本中の基本だから、一度は自分の頭で考えておいた方がいいんだよ。私ぁ若いころに出来の悪い頭でさんざん考えてきたからな。
B: ぶーぶー。
A: こんなややこしいデータ処理はnumpy様に腕をふるっていただくに限る。いい加減長くなってしまったので次回に続きます。ではでは。