例題3-2:アレかつソレまたはコレ

A: さて、比較演算子の解説をしようか。比較演算子には次のような種類がある。

a < b	aはbより小さい
a > b	aはbより大きい
a <= b	aはb以下
a >= b	aはb以上
a == b	aはbと等しい
a != b	aはbと等しくない
a is b	aはbと同一である
a is not b	aはbと同一ではない

B: うわ、雑談なしにいきなり本題なんて。

A: （無視して）上の4つは特に問題ないだろう。5つ目のa==bは、前回出てきた「aとbは等しい」を表す演算子だ。 そもそも数学で「等しい」と「代入する」の両方の意味で「=」を使うのがおかしいと言えばおかしいんだ。複数の意味をひとつの記号に持たせると混乱が起こるに決まっている。 プログラミング言語の多くでは、「等しい」と「代入する」にそれぞれ違う記号を割り振ることによって、混乱が起こらないようにしている。

B: あのー。

A: （さらに無視して）「等しくない」事を表すには!=という演算子を使う。まあこれは覚えてもらうしかないな。

B: （気を取り直して）あの、演算子は評価すると値が戻ってくるんでしたよね。これらの演算子は評価するとどんな値が戻ってくるんですか？

A: 成立する時はTrue、しない時にはFalseという値が戻ってくる。pythonインタプリタで試してみるといい。

>>> 3 <= 7
True
>>> a = 1
>>> a != 1
False

B: 雑談には反応してもらえないんですね。ぐすっ。

A: 「等しくない」はa <> bと書く事も出来るが、これは旧式の演算子で、今後は使わないことが推奨されている。 まあ他人が書いたプログラムを読む時に出くわすかも知れないので、一応知っておくと良い。

B: 「今後は」って、プログラミング言語の文法って変わるものなんですか。

A: バージョンアップの際に文法に変更が加えられることはよくある。この解説もpythonのバージョンが上がるといずれ書き直す必要が出てくるかも知れないな。

B: うわあ、そんな事になったら嫌だなあ。

A: その分、問題点が修正されたり新しい機能が加えられたりするから仕方がない。これらの演算子は、優先順位はすべて等しい。 したがって、複数並べると前回解説した通り左から順に評価される。これを比較演算子の連鎖という。

B: へ？ 複数並べる？

A: こんな具合だ。

>>> 1 <= 3 < 7 == 7 < 9
True
>>> 1 != 9 > -3
True
>>> 5 > -3 == 7
False

B: なんだか気持ち悪い…。こんなの何の役に立つんですか？

A: 変数に格納された値がある範囲内に収まっているかどうかを調べる時にはすごく便利なんだ。 例えばaとbが0以上10未満でなければならないとする。こういう時、比較演算子を連鎖出来るとこのように単一の式として書くことが出来る。 心理実験のプログラミングでもたびたび使うポイントがあると思うぞ。

>>> a = 3
>>> 0 <= a < 10
True

C言語のように比較演算子を連鎖出来ない言語の場合、次に説明する論理演算子を使って複数の式を連結しないといけない。

B: なんかこういう書き方が出来て当たり前のような気がするんですが、そうじゃないんですか。

A: んー。私が主に使う言語の中で連鎖出来るのはpythonくらいだなあ。 ちなみに、前回解説した算術演算子はすべて比較演算子より優先順位が高い。だから、以下のような式を書いた場合、掛け算や足し算が行われた後で比較が行われる。 まあ直感的な動作だと言えるね。

>>> 3*5 > 2+8
True

B: これ、先に5>2とかやられるとマズいですよね。3*True+8とかになっちゃう。エラーになるのかな？

A: なかなか面白い事を言うなあ。試してみたらわかるけど、この式ではTrueは1として計算される。Falseは0として計算される。

>>> 3*True+8
11
>>> 3*False+8
8

B: …。

A: なんでこうなるのかを言いだすと長くなるので、TrueやFalseを間違って式の中に含んでもエラーにはならないという事を覚えておくといい。 普通に心理実験のプログラムを書く限りこんな計算は不要なんだが、どうもプログラムが思ったとおりに動かなくて悩んでいたら、実は間違えてTrueやFalseが格納されている変数を計算しちゃってる場合なんかがある。 そういう時にpythonはエラーメッセージを出してくれないので注意するように。

B: うーん、不親切ですねえ。

A: 変数に値でもリストでもクラスのインスタンスでも放り込めるという便利さの裏返しだから仕方がないな。 あとisとis notという演算子があるが、これは多分心理実験のプログラムではほとんど出番がない。 一応簡単に解説しておくと、これはオブジェクトの同一性を判定する演算子だ。

B: オブジェクトの同一性？

A: 例えば以下のような比較をしてみる。

>>> a = [1,2,3]
>>> b = [1,2,3]
>>> a is b
False
>>> c = [1,2,3]
>>> d = c
>>> c is d
True

B: ？？？

A: まず最初に[1,2,3]というリストを作ってaに格納する。続いてもうひとつ[1,2,3]というリストを作ってbに格納する。 どちらも中身は同じリストだが、別々に作ったものだから同一か？と聞かれるとFalseとなる。 薄皮あんぱん5個入りの袋がふたつあったとして、どちらも薄皮あんぱんが5個入っているという意味では「同じ」だが、あくまでそれらは別の「物」だろう。だから「同一か？」と聞かれると「違う」となるわけだ。

B: これまた薄皮あんぱんとはマニアックな。

A: 続いてまた新しい[1,2,3]というリストを作ってcに格納し、dには「cの中身」を格納している。 これはいわばcというラベルが貼られた箱にdというラベルをもう一枚貼ったようなもので、「cの箱の中に入っている薄皮あんぱん」と「dの箱の中に入っている薄皮あんぱん」は「物」としても同一だ。 だから「同一か？」という質問の答えはTrueとなる。

B: うー。さっぱりわかりません。

A: きちんと理解するためには 参照 の概念を理解する必要があるだろうな。まあ、多分心理実験のプログラムでこの演算子が必要になる事はないから安心したまえ。 続いて論理演算子だ。

not a	論理否定 (aではない) (単項演算子)
a and b	論理積 (aかつb)
a or b	論理和 (aまたはb)

B: ああ、無駄な会話なしにどんどん進んでいく…

A: この辺りは解説しなくても意味はわかるだろう。優先順位は算術演算子や比較演算子より下で、この3つの中では notが一番高い。次がandで、最後がor。orはpythonの演算子で最も優先順位が低い。

B: 最低ですか。なんだか共感を感じます。

A: では使い方を見ていこうか。まずさっきの0<=a<10は、連鎖を使わない場合以下のように書く。

>>> a = 3
>>> 0 <= a and a < 10
True

B: 連鎖の方がスマートですね。

A: だろ？ この例をnotで真偽を反転させるとこのような感じになる。andよりnotの方が優先順位が高いから( )が必要な点に注意。

>>> a = 3
>>> not (0 <= a and a < 10)
False

B: あれ、( )なしでもきちんとFalseになりますよ？

>>> a = 3
>>> not 0 <= a and a < 10
False

A: それはandよりnotの方が優先順位が高いためnot 0 <= aが先に評価されているんだな。notと<=では<=の方が優先順位が高いので、まず<=から評価する。0<= aはTrue、従ってnot 0 <= aはFalse。 従ってB君の( )なしの式はFalse and a < 10となるわけだが、andは左右のどちらか一方がFalseであれば必ずFalseになる。従ってこの式の評価はFalse。偶然( )付きと( )なしの結果が一致しただけだ。

B: うー。頭パンクしそう。

A: しつこく繰り返すけど、ややこしい場合は( )できちんと括ること。それに限る。 さて、ここまで解説したら、リーディングスパンテストのプログラムを説明した時に飛ばしたキー入力の判定を説明できる。

waitingKeyPress = True
while waitingKeyPress:
    for e in event.get():
        if e.type == KEYDOWN and e.key == K_SPACE:
            waitingKeyPress = False

waitingKeyPressにTrueをセットして、この変数がFalseになるまでwhileループで待つ。いつFalseになるかというと、if文の条件式 e.type == KEYDOWN and e.key == K_SPACEがTrueになった時、というわけだ。

B: e.typeがKEYDOWNに等しく、かつe.keyがK_SPACEに等しいという条件ですね。でもこのKEYDOWNとかK_SPACEというのが何なのか、説明してもらっていないような気がするんですけど。

A: これはpygame.localsの中で定義されている定数だ。そら。

>>> import pygame.locals
>>> pygame.locals.KEYDOWN
2
>>> pygame.locals.K_SPACE
32

B: ？？？ pygame.locals.KEYDOWNの値が2ってのは、どういう事なんでしょうか。

A: pygameでは、コンピュータに起こる様々なイベントを番号で区別しているんだ。例えば何かキーボードのキーが押されると「2」というタイプのイベントが起こる。 押されていたキーが離されると「3」というイベントが起こる。「2」とか「3」では人間にはさっぱりわからないので、「2」にpygame.locals.KEYDOWNという名前をつけているんだ。 ちなみに「3」に対応している名前はpygame.locals.KEYUPだ。

B: なるほど。「2」や「3」では何のことかさっぱりわかりませんからね。じゃあpygame.locals.K_SPACEが32というのも同じことですか？

A: そう。スペースキーが押されると、「32」というキーが押されたという情報が送られてくるんだ。やはり「32」ではどのキーか分かりにくいので、pygame.locals.K_SPACEという名前を付けている。

B: ふむふむ。じゃあすべてのキーに対して番号が割り振られているんですか？

A: こんな感じだな。

K_UNKNOWN	0	K_a	97	K_DOWN	274
K_BACKSPACE	8	K_b	98	K_RIGHT	275
K_TAB	9	K_c	99	K_LEFT	276
K_CLEAR	12	K_d	100	K_INSERT	277
K_RETURN	13	K_e	101	K_HOME	278
K_PAUSE	19	K_f	102	K_END	279
K_ESCAPE	27	K_g	103	K_PAGEUP	280
K_SPACE	32	K_h	104	K_PAGEDOWN	281
K_EXCLAIM	33	K_i	105	K_F1	282
K_QUOTEDBL	34	K_j	106	K_F2	283
K_HASH	35	K_k	107	K_F3	284
K_DOLLAR	36	K_l	108	K_F4	285
K_AMPERSAND	38	K_m	109	K_F5	286
K_QUOTE	39	K_n	110	K_F6	287
K_LEFTPAREN	40	K_o	111	K_F7	288
K_RIGHTPAREN	41	K_p	112	K_F8	289
K_ASTERISK	42	K_q	113	K_F9	290
K_PLUS	43	K_r	114	K_F10	291
K_COMMA	44	K_s	115	K_F11	292
K_MINUS	45	K_t	116	K_F12	293
K_PERIOD	46	K_u	117	K_F13	294
K_SLASH	47	K_v	118	K_F14	295
K_0	48	K_w	119	K_F15	296
K_1	49	K_x	120	K_NUMLOCK	300
K_2	50	K_y	121	K_CAPSLOCK	301
K_3	51	K_z	122	K_SCROLLOCK	302
K_4	52	K_DELETE	127	K_RSHIFT	303
K_5	53	K_KP0	256	K_LSHIFT	304
K_6	54	K_KP1	257	K_RCTRL	305
K_7	55	K_KP2	258	K_LCTRL	306
K_8	56	K_KP3	259	K_RALT	307
K_9	57	K_KP4	260	K_LALT	308
K_COLON	58	K_KP5	261	K_RMETA	309
K_SEMICOLON	59	K_KP6	262	K_LMETA	310
K_LESS	60	K_KP7	263	K_LSUPER	311
K_EQUALS	61	K_KP8	264	K_RSUPER	312
K_GREATER	62	K_KP9	265	K_MODE	313
K_QUESTION	63	K_KP_PERIOD	266	K_HELP	315
K_AT	64	K_KP_DIVIDE	267	K_PRINT	316
K_LEFTBRACKET	91	K_KP_MULTIPLY	268	K_SYSREQ	317
K_BACKSLASH	92	K_KP_MINUS	269	K_BREAK	318
K_RIGHTBRACKET	93	K_KP_PLUS	270	K_MENU	319
K_CARET	94	K_KP_ENTER	271	K_POWER	320
K_UNDERSCORE	95	K_KP_EQUALS	272	K_EURO	321
K_BACKQUOTE	96	K_UP	273

B: うわっ。すごい。

A: キー名を見ればだいたいどのキーと対応しているかわかるだろう。 少しコメントしておくと、左端の列のK_0～K_9はキーボードの左上から並んでいる1から0までのキーだ。それに対して中央の列のK_KP0～K_KP9は独立した10キーの0～9だ。 K_LSHIFTとK_RSHIFT、K_LCTRLとK_RCTRL、K_LALTとK_RALTなどはそれぞれ左Shiftキーと右Shiftキー、左Ctrlキーと右Ctrlキー、左Altキーと右Altキーといった具合に、LとRで左右のキーを区別している。

B: 左右のShiftキーとかもちゃんと区別できるんですね。これは便利そうだ。

A: もちろんPCに接続されているキーボードに10キーがなければ、そのPCではK_KP0などのキー番号が生じることはない。 「zかxのキーが押された場合にwhileループを抜ける」とか、いろいろと条件を変えてプログラムを書いてみるといい練習になるよ。

B: はーい。

A: ふう、これで比較演算子と論理演算子の解説はだいたいOKかな。ついでだからビット演算子も説明しておくか。

~a	論理否定 (aではない) (単項演算子)
a<<b, a>>b	ビット単位のシフト
a & b	ビット単位の論理積
a ^ b	ビット単位の排他的論理和
a | b	ビット単位の論理和

B: ビット単位って何ですか？

A: んー。特にビット単位の論理和は結構使われるのでここで一応解説しておくべきかなあと思って出したけど、多分心理実験のプログラムを書く時に使う事は少ないと思う。 とりあえず簡単な心理実験のプログラムが書ければいいという人は、以下を読み飛ばしてもいいかも知れない ね。 とにかく、ビット単位の演算と言うのは数を2進数で表現して、それぞれの桁毎に演算を行うということなんだ。

B: ？？？

A: 数字を2進数で表記すると、1と0の列になる。これをスイッチに見立てて、1をON、0をOFFとしよう。 そうすると、たくさんのスイッチがズラリと並んだ機械の状態を2進数で表現できることになる。例えば4つのスイッチがあるとして、すべてOFFなら0000、左端と右端のスイッチだけONなら1001だ。ここまではいいかな？

B: はぁ。なんとなく。

A: 4つのスイッチが並んでいる場合、そのON/OFFの組み合わせは16通りある。ON/OFFを2進数で表現する方法を使うと、この16通りのスイッチの状態を自然に0000～1111の2進数に対応させる事が出来る。0000～1111は10進数で書くと0～15だ。

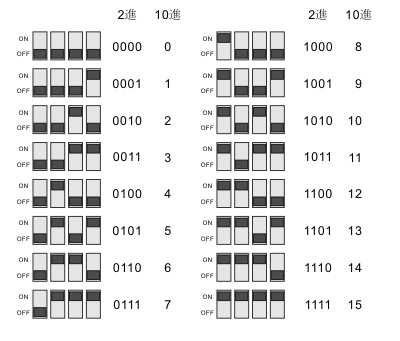
B: ううっ。高校生の時の苦い思い出が。こういうの苦手だったんです。

A: とにかく2進数を使うと多数のスイッチの状態と整数を自然に対応させる事が出来ることを納得してもらえればそれでいい。 さて、ビット単位の論理演算と言うのは、2進数に対して以下のような演算を行うことを指す。

論理否定	単項演算子	すべての桁について、0と1を反転
論理積	二項演算子	ふたつの2進数の対応する桁それぞれに対して、どちらも1ならば1、それ以外は0
論理和	二項演算子	ふたつの2進数の対応する桁それぞれに対して、どちらか一方が1であれば1、それ以外は0
排他的論理和	二項演算子	ふたつの2進数の対応する桁それぞれに対して、どちらか一方だけ1であれば1、それ以外は0

B: あーうー。スイッチの話と何の関係があるのかさっぱりわかりません。

A: ビット単位の論理演算をうまく使うと、特定のスイッチをON/OFF出来るのさ。 例えばこの4つのスイッチは左から順に4階、3階、2階、1階のエアコンのスイッチだとしよう。 それで、floor1～floor4という変数にそれぞれの階のスイッチだけがONになっている状態に対応した数を入れておく。具体的には2進数で0001,0010,0100,1000。10進数で書くと1,2,4,8だな。 ちなみにこれは2の0乗、1乗、2乗、3乗に対応している。

>>> floor1 = 1
>>> floor2 = 2
>>> floor3 = 4
>>> floor4 = 8

このように準備しておけば、論理和を使って複数のフロアのスイッチを自由自在にONに出来る。たとえば1階と4階をONにしたい場合はこうだ。

>>> floor1 | floor4
9

上の図と見ればわかるが、2階と4階がONになっている状態に対応している10進数は「9」だ。 論理和をとる事で非常に直感的にスイッチの状態に対応する数を求められることがわかる。

B: あのー。[1,0,0,1]というリストを使った方が分かりやすいと思うんですけど。

A: うむ。確かに人間にはその方が分かりやすいね。でもコンピュータにとってはビット単位で指定された方が都合がいい場合も多いんだ。 だからいろんなプログラムを書いているとこういった論理演算が求められる場面にである事がある。

B: むう。コンピュータとは分かり合えそうにないなあ。

A: まあ、心理実験のプログラムを書く限りでは、複雑なビット単位の論理演算をすることはほとんどないだろう。 将来仕事の都合でC++を使ってDirectXを使ったプログラミングとかしなきゃいけなくなったりしたら、その時には役に立つかも知れない。

B: えー。そんな仕事あるんですか。

A: 私は昔まさにそういう仕事をしていたんだがね。CやC++も今となってはずいぶん古臭い言語になってしまったが、 それでも使われ続けているのはCやC++で書いた方がいいプログラムがまだまだ残ってるからなんだよ。

B: はー。理解できない世界だ。

A: これでビット単位の論理演算子の解説も終わりにするか。次はリストの演算子を解説しよう。