5. Pythonコードを書いてみよう―視覚の空間周波数特性¶
5.1. この章の実験の概要¶
この章では、視覚の時空間特性の計測実験を題材として、Builderによる実験にPythonコードを組み込む方法を解説します。グラフィカルユーザーインターフェース(GUI)で実験を作成出来る事がBuilderの長所ですが、正直なところ本格的な実験をしようとすると「あれが出来ない、これが出来ない」という事だらけであまり役に立ちません。しかし、BuilderにPythonのコードを組み合わせることによって、飛躍的に「出来る事」の幅が広がります。プログラミングの経験がない方には最初かなり難しく感じられるかもしれませんが、実際に実験を動かしながら少しずつ理解を深めてください。
この章の実験では、視覚の空間周波数特性を取り上げます。「空間周波数」という用語は 第4章 で紹介しましたね。皆さんは、視力検査であまりにも小さな視標は知覚できない事を経験していると思います。視標が小さいということは狭い範囲内で明暗が大きく変化するということですから、「空間周波数」という用語を使えば「空間周波数が高すぎる視覚刺激は私たちには知覚できない」と表現できます。視力検査では高空間周波数の刺激がどこまで知覚できるかしか調べませんが、実は空間周波数が低すぎる刺激に対しても私たちの視覚の感度が低下することがわかっています。この章では、空間周波数の変化に応じて私たちの視覚の感度が変化することを確認する実験を作成します。便宜上「実験」と呼んでいますが、ベースになっているのは筆者が以前に知人から紹介してもらったゲーム風のデモです。正確な感度の計測に適した手続きではありませんが、PythonのコードをBuilderに組み込む最初の一歩として適しているので取り上げました。
なお、この実験では刺激の視角が非常に重要な意味を持ちますので、 [単位] にdegを使用します。モニターの観察距離の設定などをしっかりおこなっておいてください(第2章 参照)。
図5.1 に使用する刺激を示します。スクリーン中央に直径0.1degの白色の小さな円を提示します。実験中、実験参加者はこの刺激を固視し続けないといけません。この刺激を固視点と呼ぶことにします。固視点から視角で5.0deg離れた位置に、直径4.0degの時計回りまたは反時計回りに15度傾いたグレーティング刺激を1.0秒提示します。この刺激をターゲットと呼ぶことにします。ターゲットの出現方向は固視点の右を0度として反時計回りに0度、45度、90度、135度、180度、225度、270度、315度の8方向の中から無作為に選びます。グレーティングの空間周波数は0.2、0.4、0.8、1.6、3.2、6.4、12.8 cpd (cyecle per degree: 視角1度あたりの繰り返し回数)の7種類を用います。
図5.1 実験に使用する刺激。¶
図5.2 に実験の手続きを示します。試行開始時には、スクリーン中央に固視点のみが提示されています。実験参加者がカーソルキーの左右どちらかを押すと、1秒後にターゲットがいずれかの位置に出現します。ターゲットの色はキーが押された直後には$[0,0,0]、すなわち背景と全く同一で知覚することが出来ませんが、6秒間かけて一定の速度で$[1,1,1]まで変化します。視覚刺激の明暗差のことをコントラストと言いますが、この用語を使えばターゲットのコントラストが上昇していくと表現できます。実験参加者は、ターゲットがどちらに傾いているかを知覚出来たら出来るだけ速く、反時計回りであればカーソルキーの左、時計回りであれば右のキーを押します。キーが押されるとターゲットは消えて、直ちに次の試行に進みます。ターゲット出現後6秒経過しても反応がなかった試行はエラーとして記録して、やはり直ちに次の試行に進みます。時間と共にターゲットのコントラストが上昇するので、実験参加者の反応時間が早いほど低いコントラストでターゲットを知覚出来たと考えられます。以上の手続きを、すべてのターゲット方向(8種類)とターゲット空間周波数(7種類)の組み合わせに対して反時計回りを1回、時計回りを1回、合計8×7×2×2＝112試行行います。途中に休憩を挟まずに一気に実行し、すべての試行が終了すれば実験は終わりです。
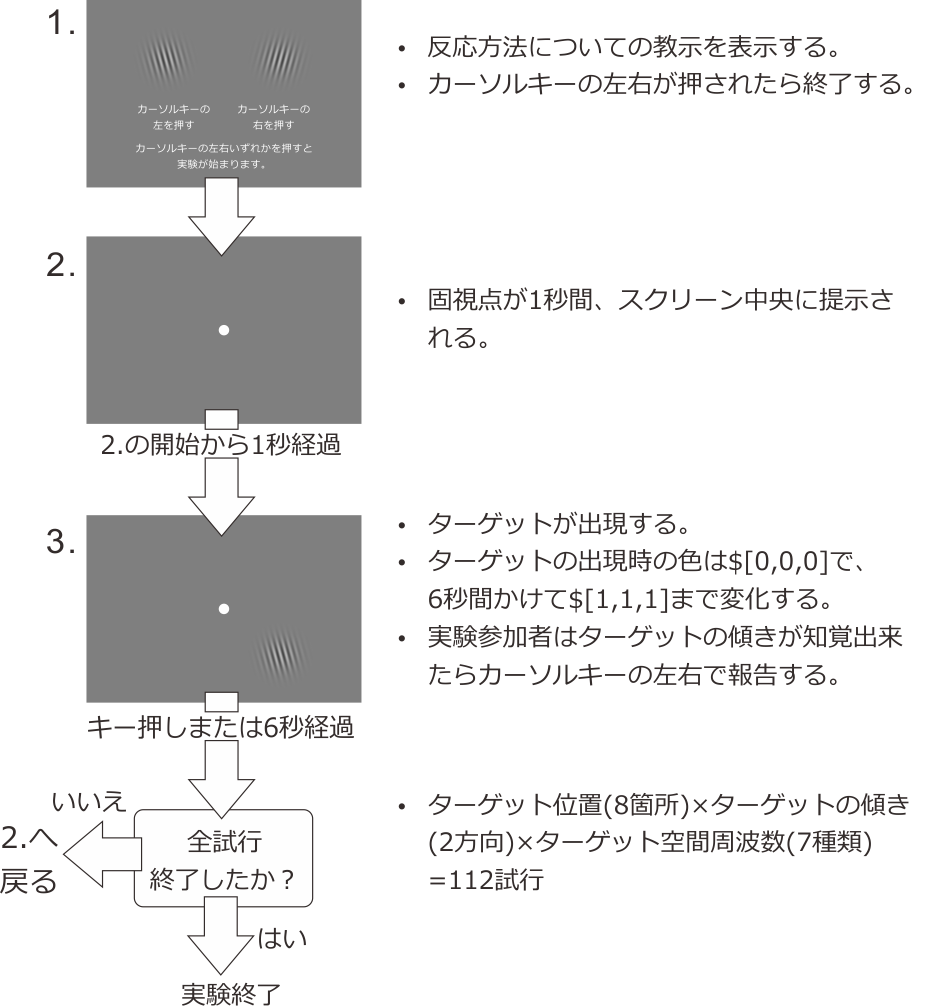
図5.2 実験の手続き。¶
最初に述べたとおり、この手続きは正確な感度を計測することよりも、簡単な手続きで空間周波数による感度の違いを感じるためのデモと言った方が適切です。この手続きでは試行数が少なすぎますし、なにより参加者の反応時間からターゲットを検出できる閾値のコントラストを測定しようという発想自体が正確な測定に適していません。というのも、反応時間には実際にターゲットが知覚出来てからキーを押すまでの時間などが含まれて、その間にもターゲットのコントラストは上昇し続けているからです。正確さを期するのであれば 第4章 のような恒常法の手続きを用いるべきです。この章の実験は、あくまでBuilderをマスターするための例題だと考えてください。
第4章 までに解説したテクニックでは、時間の経過とともにだんだんコントラストが上昇するグレーティングを提示するのは困難です。持続時間が0.1秒程度のルーチンを作成して、0.1秒毎のコントラストの値を並べた条件ファイルを作成して、sequentialのループを用いて次々とコントラストを変更していけば提示自体は不可能ではありません。しかし、キーが押されたらその時点で提示を中断するのはこの方法では出来ませんし、なにより実験記録ファイルに全試行0.1毎にキーが押されただの押されなかっただのという記録が出力されてしまうのでデータ処理の時点で悲惨なことになります。この章では、Builderの実験にPythonのコードを組み込むことで問題を回避します。まずは、 第4章 までに解説済みの作業で出来るところまで実験を作成しましょう。以下のように実験を作成してexp05a.psyexpの名前で保存するものとします。
実験設定ダイアログ
「xlsx形式のデータを保存」をチェックする。
[単位] をdegにする。モニターの設定(観察距離、モニターの幅長および解像度)をまだ設定していない場合は:numref:第%s章 <chapter-draw-basic-stimuli> を参考にモニターセンターを開いて設定する。
trialルーチン
Gratingコンポーネントをひとつ配置し、以下のように設定する。
[名前] をtargetStimにする。
[マスク] をgaussにする。
[回転角度 $] をtargetDirにして、「繰り返し毎に更新」にする。
[空間周波数 $] をtargetSFにして、「繰り返し毎に更新」にする。
[サイズ [w, h] $] を[4.0, 4.0]にする。
[テクスチャの解像度 $] を512にする。
Keyboardコンポーネントをひとつ配置し、 [検出するキー $] を'left', 'right'にする。 [正答を記録] をチェックして、 [正答] に$correctAnsと入力する。
Polygonコンポーネントをひとつ配置し、 [名前] をfixationにする。 [形状] を正多角形、 [頂点数] を12、 [サイズ [w, h] $] を[0.1, 0.1]にする。
すべてのコンポーネントの [終了] を実行時間 (秒)で6.0にする。
instructionルーチン(作成する)
フローの先頭に挿入する。
Gratingコンポーネントを2個配置し、 [名前] をright_sample、left_sampleとする。以下のように設定する。
[マスク] をgaussにする。
[空間周波数 $] を1.0にする。
[サイズ [w, h] $] を[4.0, 4.0]にする。
[テクスチャの解像度 $] を512にする。
left_sampleの [位置 [x, y] $] を[-5.0, 0.0]とする。right_sampleの [位置 [x, y] $] を[5.0, 0.0]とする。
left_sampleの [回転角度 $] を-10.0にする。right_sampleの [回転角度 $] を10.0にする。
Textコンポーネントを3個配置して、Letter height $を適当な値(0.5など)にする。ひとつをleft_sampleの下に位置するようにして [文字列] に「反時計回り」と入力する。別のひとつをright_sampleの下に位置するようにして [文字列] に「時計回り」と入力する。最後に残ったTextコンポーネントの [文字列] に、反時計回りならばカーソルキーの左、時計回りならば右を出来るだけ速く押して反応するように教示するメッセージを入力する。
Keyboardコンポーネントをひとつ配置し、 [検出するキー $] を'left', 'right'にして [記録] を「なし」にする。
全てのコンポーネントの [終了] を空白する。
blankルーチン(作成する)
フローのinstructionルーチンとtrialルーチンの間に挿入する。
Polygonコンポーネントをひとつ配置し、 [名前] をfixation_2にする。 [形状] を正多角形、 [頂点数] を12、 [サイズ [w, h] $] を[0.1, 0.1]にする。 [終了] を「実行時間 (秒)」で1.0にする。
trialsループ(作成する)
blankルーチンとtrialルーチン繰り返すように挿入する。
[繰り返し回数 $] の値を1にする。
[繰り返し条件] にexp05cnd.xlsxと入力する。
exp05cnd.xlsx (条件ファイル)
targetSF、targetDir、correctAns、targetPosの4パラメータを設定する。
実験手続きの説明を満たすようにtargetSFに7種類の空間周波数、targetDirに2種類の傾きの値を入力する。targetDirと対応するようにcorrectAnsに値を入力する(targetDirが-15の行は'left'、15の列は'right')。targetPosはとりあえず空白にしておく。この時点でパラメータ名の行を除いて14行となる。
blankというルーチンではただ1秒間固視点を提示しているだけです。これは実験手続きの「1秒間固視点が提示される」という点を実現するために挿入されているのですが、blankルーチンが無くてもtrialルーチンでtargetStimの [開始] をfixationの [開始] から1秒遅らせれば実現できます(第3章 参照)。しかし、このテクニックを使うと後でコントラストを時間の経過とともに上昇させる処理の解説がかなり複雑になってしまいますので、今回は固視点の提示のために独立したルーチンを使用しています。
これで準備が整いました。いよいよPythonのコードをBuilderに追加しますが、その前に用語の説明をしておきましょう。退屈かもしれませんが、用語を覚えておかないと後の解説がわからないのでしっかり覚えてください。
5.2. 変数、データ型、関数といった用語を覚えよう¶
第3章 でPythonにおける「名前」の話が出てきたことを思い出してください。刺激にstimulus、刺激色を表すパラメータにstim_colorという「名前」を付けて、「stimulusの [色] プロパティにstim_colorの値を代入する」とかいったことをしたのでした。この時に敢えて触れなかったのですが、この「名前」は一体何の名前なのでしょうか。「えっ、今『刺激』や『パラメータ』に名前を付けたって言ったじゃないか」と言われるかも知れません。確かにその通りなのですが、より正確に言うと、これらのものを収納しておく「箱」に名前をつけたのです。stimulusという名前の「箱」にPolygonコンポーネントを収納したり、stim_colorという名前の「箱」に色の値を収納したりしていたのです。この名前は「箱」の名前なのですから、当然中身を入れ替えることも出来ます。第3章 の実験でループの繰り返しの度に刺激色が変化していたのは、Builderが毎回stim_colorという箱の中におさめられた値を変更してくれていたからです( 図5.3 )。この箱のことを変数と呼びます。今まで「名前」と呼んでいたものは変数の名前、すなわち変数名です。
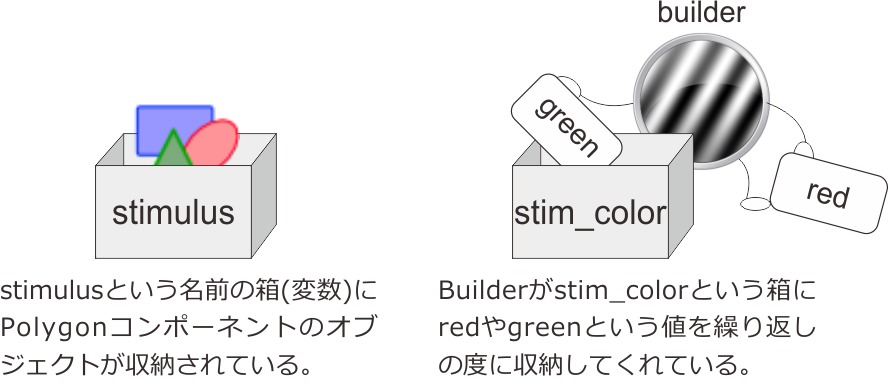
図5.3 変数とはいろいろなものを収納しておける箱のようなもの。¶
Pythonでは、変数の中にさまざまなものを収納することが出来ます。C言語のように変数に「型」がある言語では、整数値を入れる変数には整数値のみ収納できるといった制限がありますが、Pythonにはそのような制限がありません。Pythonで扱える型のデータであればすべて収納できます。プログラミングを学んだ経験がない方は「データの型ってなんだ？」と思われるかもしれませんね。ほとんどのプログラミング言語では、扱うことが出来るデータにいくつかの「型」があって、型によって適用できる処理が異なります。 表5.1 に基本的なPythonの型を示します。ここでそれぞれの型を詳しく説明し出すとなかなか実験の作成にたどり着きませんので、ごく簡単な説明に止めています。ここで注目していただきたいのは「シーケンス」という型です。他のプログラミング言語を学んだことがある方は「配列」という名前の方がピンと来るかもしれません。第2章 で刺激の色をRGB値で指定したり、刺激の位置や大きさを指定したりする時に「両端の角括弧は意味があるので忘れずに入力してください」と書きましたが、実はこれはシーケンスの一種である「リスト」を書くときのPythonの文法なのです。[1.0, 0.0, 0.5]と書かれていたら、Pythonはこれをリストとして解釈して「最初の要素は1.0、その次は0.0、最後は0.5」という具合にそれぞれの値を取り出すことが出来ます。[ ]が欠けているとリストとして解釈することが出来ないのでエラーとなるわけです。
型 |
概要 |
|---|---|
数値 |
単一の数値。Python内部では整数のみを扱う型(整数型)と小数点つきの数値を扱う型(浮動小数点型)がある。 |
文字列 |
アルファベットやかな文字、漢字、各種記号等の文字が連なったもの。Python2と3で大きく異なる。本書の解説はPython3を前提としてる。Python2の文字列については「 5.7.3:Python2とPython3の文字列の違い(上級) 」参照のこと。 |
シーケンス(リスト、タプル) |
複数のデータを順番に並べてひとまとめにしたもの。「2番目の要素を取り出す」といった具合に位置を指定して内容を取り出すことが出来る。カンマで区切られた要素を[ ]で囲んだものをリスト、( )で囲んだものをタプルと呼ぶ。 |
辞書 |
複数のデータをひとまとめにして、キーと呼ばれる値を用いて内容を取り出せるようにしたもの。第4章 で実験情報ダイアログの入力値を保持していたexpInfoという変数に格納されているデータがこれに該当する。 |
データ型の詳細については必要に応じて解説することにして、最後に関数という用語に触れておきましょう。関数と聞くと、数学の授業で習った「yはxの関数」とか「2次関数のグラフ」といった内容を思い出される方も多いと思います。例えば「zはxとyの関数」と言った場合、xとyの値が与えられたら、その関数で定められた計算を行えば対応するzの値を得ることが出来ます( 図5.4 左)。Pythonの関数とはこの関係を一般化したようなものです。例えば、「ファイルを保存する」という関数があるとします。この関数にファイル名と保存したいデータを与えると、ファイルを作成したりデータを書きこんだりといった処理が行われて、保存が成功したか否かを示す値が得られるとします( 図5.4 右)。ずいぶん数学で習った関数と違うような感じがするかもしれませんが、「値を入力すると定められた処理が行われて結果が出力される」という構図はよく似ています。このような働きを持つものをPythonでは関数と呼びます。関数に入力する値のことを引数、出力のことを戻り値と呼びます。実は関数にもいろいろな種類があるのですが、それについても今後必要に応じて説明することにして、関数、引数、戻り値という用語を覚えておいてください。
図5.4 数学で習った関数とPythonにおける関数。¶
- チェックリスト
変数の役割を説明できる。
関数の役割を、引数、戻り値という用語を用いながら説明できる。
5.3. 数学関数を利用して刺激の位置を指定しよう¶
退屈な用語の説明はいったん切り上げて実験の作成に戻りましょう。まず、Builderでexp04a.psyexpを開いて、trialルーチンのtargetStimのプロパティ設定ウィンドウを開いてください。先ほどの作業では、まだtargetStimの [位置 [x, y] $] が初期値のままに残されていました。刺激の位置は固視点から半径5.0degの円周上で、右方向を0度として0度から45度間隔で8方向の中から無作為に選ぶのでした。試行毎に変化するのですから条件ファイルにこれら8種類の位置を書きこまなければいけないのですが、45度や135度の方向のx座標、y座標の値を書きこむのが少々面倒です。半径が5.0ですから、45度の方向はx座標、y座標とも5.0×1/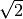 
=3.53553…です。幸い135度や225度の方向は符号を変えたらいいだけですのでこの程度なら手入力してもいいのですが、後々半径を変更したくなったり45度間隔の代わりに60度間隔にしたくなったりした時に面倒です。なにより実験記録ファイルを見たときに刺激位置のパラメータが3.53553, 3.53553と書かれているよりも45と書かれていた方が圧倒的にわかりやすいでしょう。そこで、さっそく関数を用いて条件ファイルに45とか135とか書けばBuilderが座標値を計算してくれるように改造してみましょう。
sin(x) |
正弦関数 |
min(x,y,z…) |
x, y, z,…の最小値 |
cos(x) |
余弦関数 |
max(x,y,z…) |
x, y, z,…の最大値 |
tan(x) |
正接関数 |
average(x) |
xの平均値 |
log(x) |
自然対数関数 |
std(x) |
xの標準偏差 |
log10(x) |
常用対数関数 |
deg2rad(x) |
xを度からラジアンに変換 |
pi |
円周率 |
rad2deg(x) |
xをラジアンから度に変換 |
sqrt(x) |
平方根 |
視覚刺激を用いた知覚や認知の実験では、三角関数や指数関数の数学関数や円周率などの定数はしばしば用いられるので、Builderでは 表5.2 に示す関数が用意されています。今「三角関数や指数関数」と書いたばかりなのに指数関数がないじゃないか、と思われるかも知れませんが、これ以外の数学関数を使用するには:numref:第%s章 <chapter-code-if> で解説するコンポーネントを使う必要があります。この点については「 5.7.1:他の数学関数を使用する方法 」も参照してください。さて今回の目的の場合、条件ファイルに書かれた角度から座標値を計算するのですから、deg2rad( )とsin( )、cos( )が役に立ちそうです。まずは45度のsinを計算する式を作るところから始めてみましょう。数学でxの関数f(x)に対してxに3を代入する時にf(3)と書いたように、deg2rad( )を用いて45度をラジアンに変換するにはdeg2rad(45)と書きます。座標値を計算するにはラジアンに変換した値をsin( )およびcos( )に代入する必要がありますが、Pythonを含む多くのプログラミング言語では、関数の引数に他の関数(の戻り値)を用いることが許されています。このテクニックを使うと、sin( deg2rad(45) )と書けば「まずdeg2rad(45)を計算して、その結果をsin( )に代入する」という計算が出来ます( 図5.5 )。同様に、45度のcosはcos( deg2rad(45) )という式で計算ができます。
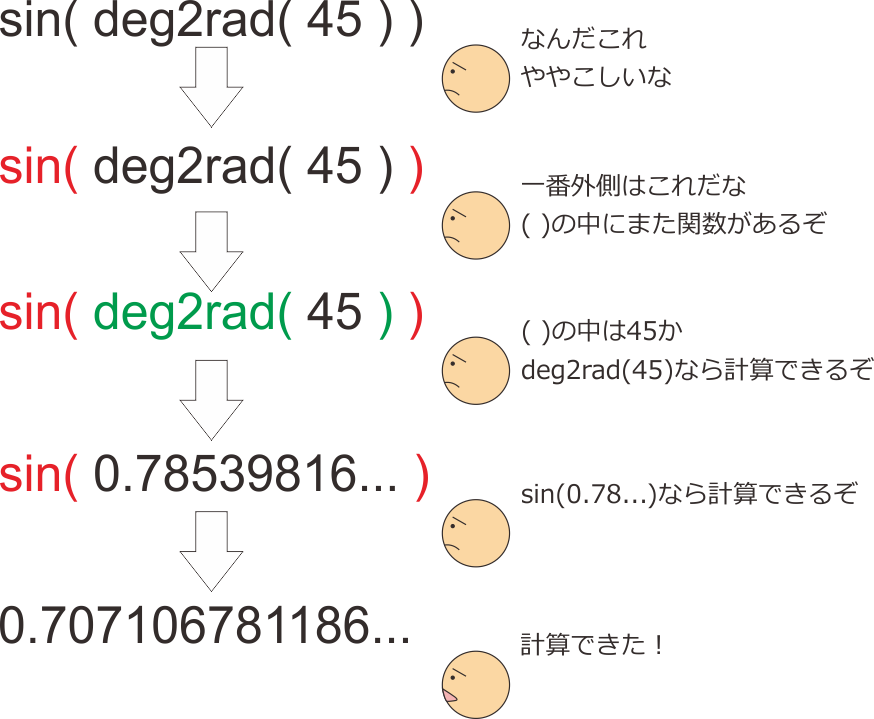
図5.5 関数の引数に関数を書くとPythonが順番に計算をします。¶
これで45度のsinとcosを計算する式が出来ましたが、目的の座標値を得るためにはこれらの式に半径の値、5.0を掛けなければいけません。数値同士の足し算や掛け算を行うには、算術演算子と呼ばれる記号を用います( 表5.3 )。また難しそうな用語が出てきたと思われるかもしれませんが、要するに+とか-とかいった記号のことです。昔のタイプライターで×や÷といった記号を使えなかった名残で、掛け算は * 、割り算は / と書くことに決まっています。この算術演算子を利用すれば、ようやく45度の時の座標値を計算する式を完成させることが出来ます。 [位置 [x, y] $] に書くときにはx座標、y座標の値をこの順番に並べたリストにしなければいけないことに注意すると、以下の式が得られます。
[5*cos(deg2rad(45)), 5*sin(deg2rad(45))]
x + y |
x足すy |
-x |
xの符号を反転 |
x - y |
x引くy |
x % y |
Xをyで割った余り |
x * y |
x掛けるy |
x ** y |
Xのy乗 |
x / y |
x割るy |
x // y |
x割るy(割り切れない場合は切り上げ) |
これでターゲットの方向が45度の時の式が完成しましたが、今回の実験では条件ファイルから角度を読み込んで座標値を計算しないといけません。幸い、関数の引数には変数を書くことが出来るので、単に先ほどの式の45を変数名に書き換えるだけでこの目標は達成できます。先ほど条件ファイルを作成した時に空白のまま残しておいたtargetPosを利用することにしましょう。Builderを開いてtrialルーチンのtargetStimの [位置 [x, y] $] に以下のように入力し、「繰り返し毎に更新」にしてください。
[5*cos(deg2rad(targetPos)), 5*sin(deg2rad(targetPos))]
Builderでの変更を終えたら条件ファイルexp05cnd.xlsxを開いてください。すでに14行分の条件が入力されていますが、これらの14条件を8種類(0, 45, 90, 135, 180, 225, 270, 315)のtargetPosすべてに対して実行するように変更してください。最終的に14×8=112行の条件ファイル(パラメータ名の行を除く)になるはずです。
以上で刺激の位置を試行毎に決定することが出来るようになりました。あとは時間の経過とともにだんだんコントラストが高くなる刺激を実現出来れば実験は完成します。また新しい話が出て来るので、ここでいったん解説を区切ることにしましょう。
- チェックリスト
Builderで使用できる数学関数を挙げることが出来る
関数の引数に別の関数の戻り値を使うことが出来る。
条件ファイルから読み込んだパラメータ値を関数の引数に使うことが出来る。
Pythonの算術演算子8つ挙げてその働きを説明することが出来る。
5.4. ルーチン開始後の時刻を取得して刺激を変化させよう¶
時間の経過とともに刺激のコントラストを上昇させるには、「現在の時刻に応じて [色] の値を変更する」ことと、「 [色] の変化を刺激に反映させる」ことが必要です。第一の点については、t というBuilderの内部変数を利用します。内部変数とはBuilderが正常に動作するためにユーザーから見えない内部で自動的に作成する変数で、t には現在のルーチンが開始されてから何秒経過したかが保持されています。第二の点については、各プロパティの値を入力する欄の右側のプルダウンメニューで「フレーム毎に更新する」を選択することで実現できます。ごくシンプルな実験を作成してこれらのことを確認してみましょう。
一旦exp05a.psyexpを保存して、新規に実験を作成してください。trialsルーチンにTextコンポーネントをひとつ配置して、Textコンポーネントの [終了] を「実行時間 (秒)」にして値に10.0と入力して [文字列] に $t と入力してください。そして、 [文字列] の右端のプルダウンメニューを「フレーム毎に更新」にしましょう( 図5.6 )。これだけで準備はOKですので、適当な名前で保存して実行してみてください。スクリーン中央に、ものすごい速さで0.0から10.0に向かって上昇していく数値が表示されるはずです。試しに「フレーム毎に更新する」を今までの章で使ってきた「繰り返し毎に更新」に変更して、0から全く値が変化しないことを確認しておいてください。なお、小数点以下2桁目まで表示したいなど、小数の表示を変更する方法については 第12章 で扱います。
一般論として、リアルタイムに刺激の色や位置といったプロパティを変更すると、PCのグラフィック機能への負担が大きくなります。ですから「更新しない」や「繰り返し毎に更新」に設定された刺激については、Builderはルーチン開始時に刺激を作成した後、一切プロパティ値を変更しません。近年の高性能なPCならば、刺激数が数百、数千個でもない限り全て「フレーム毎に更新する」にしてもほとんど問題なく処理できるでしょうが、実験中は少しでもPCに無用な処理はさせないようにしてPCの処理遅れなどを防ぎたいところです。実験の性質上どうしてもリアルタイムに値を変化させないといけないプロパティに関してだけ「フレーム毎に更新する」を設定するようにしましょう。
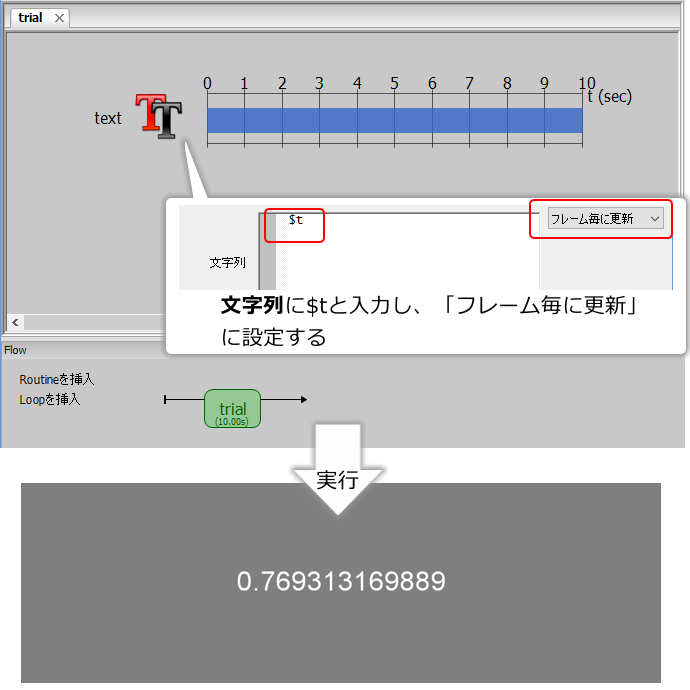
図5.6 Builderの内部変数 t のテスト。画面上にルーチン開始から経過した時間が表示されます。¶
Builderの内部変数 t と「フレーム毎に更新する」を用いれば、時間と共にコントラストを変化させることは難しくありません。Builderでexp05a.psyexpを開いてtrialルーチンのtargetStimのプロパティ設定ダイアログを開いてください。ルーチン開始時に [色] が$[0.0, 0.0, 0.0]で、一定の速度で上昇して6.0秒経過した時点で$[1.0, 1.0, 1.0]になればよいのですから、$[t/6.0, t/6.0, t/6.0]とすれば目的を達成できるはずです。忘れずに「フレーム毎に更新する」の設定もしてください。これで実験が完成しました。
実験を実行したら、targetSFの値別に反応時間の平均値を計算してみてください。ひとつのtargetSFの値に対してtargetDirが2種類、targetPosが8種類で16試行あるはずです。平均値を計算したら、横軸にtargetSF、縦軸に反応時間の平均値をプロットしてみましょう。実験に使用したモニターの平均輝度や部屋の照明などによって結果は変化しますが、targetSFが1.6か3.2辺りで反応が最も速く、最小値の0.2や最大値の12.8では反応が遅くなります( 図5.7 左)。反応時間が遅いという事はそれだけターゲットのコントラストが高くならないと刺激の傾きが判断できないということですから、ターゲットの空間周波数が高すぎても低すぎても視覚の感度が低下することがわかります。縦軸を反応時間の逆数にすると、一般的な空間周波数別の感度のグラフの形状に近くなります( 図5.7 右)。
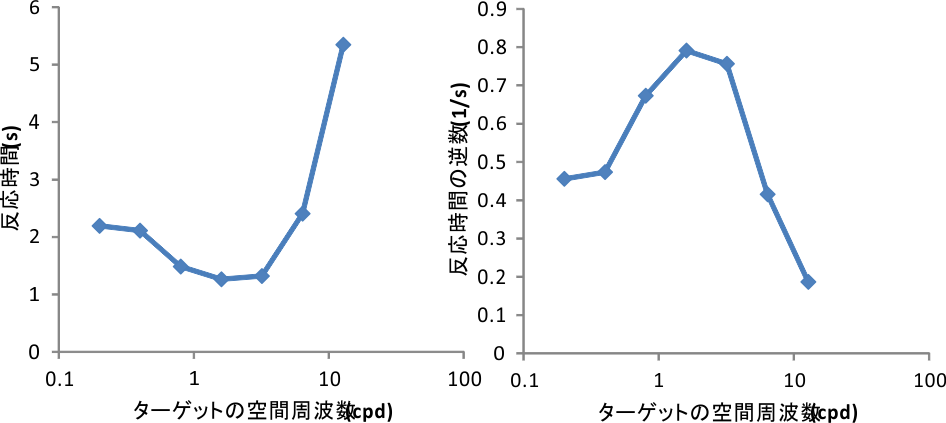
図5.7 実験結果の例。左は反応時間、右は反応時間の逆数を縦軸にプロットしています。横軸が対数軸になっている点に注意してください。¶
ここでこの章の内容は一区切りですが、次の話題に移る前にひとつ補足します。Builderでは現在のルーチンが開始してから経過した時間を t という変数に保持していると述べましたが、同時にルーチンが開始してからのフレーム数を frameN という変数に保持しています。 [開始] や [終了] をフレーム数で指定している場合は、tよりもframeNを使用する方が便利でしょう。フレーム数による [開始] や [終了] の指定については「 2.10.5:時刻指定におけるframeについて 」を参考にしてください。
- チェックリスト
現在のルーチンが開始してから経過した時間を保持しているBuilderの内部変数を答えられる。
現在のルーチンが開始してから描画したフレーム数を保持しているBuilderの内部変数を答えられる。
現在のルーチンが開始してから経過した時間の値を用いて、時間の経過とともに色や位置が変化する実験を作成することが出来る。
5.5. 実験情報ダイアログから実験のパラメータを取得しよう¶
この章で目指した実験はすでに完成していますが、応用問題ということで少し改造してみましょう。第4章 で実験情報ダイアログから条件ファイル名を取得しましたが、同様に刺激の位置や色といったプロパティ値を取得することが可能です。ただ、実験情報ダイアログで数値を入力してプロパティ値として使う場合は少し工夫が必要です。この点を解説するために、exp05a.psyexpを改造してtaregtStimの大きさと、固視点からの距離を実験情報ダイアログで変更できるようにしてみましょう。exp05a.psyexpを開いてexp05b.psyexpという別名で保存し直してください。
図5.8 に作業の概要を示します。実験情報ダイアログに追加する項目のうち、targetStimの大きさを入力する項目をeccentricity、固視点からの距離を入力する項目をtarget sizeという名前にすることにしましょう。ちなみにeccentrictyとは、視覚刺激が視野中心からどれだけ外れた位置にあるかという意味です。また、target sizeという項目名にはスペースが入っていますが、実験情報ダイアログの項目名はPythonの変数名でなくてもかまわないのでこのようにスペースが入っていてもエラーになりません。方法がわからない人は 第4章 を復習しましょう。
続いてtargetStimのプロパティ設定ダイアログを開いて、 [位置 [x, y] $] と [サイズ [w, h] $] で実験情報ダイアログの値を参照するように変更します。第4章 の内容を思い出すと、expInfo['eccentricity']と書けばその値が取り出せるはずです。取り出した値は [位置 [x, y] $] に入力済みの式の5に相当しますから、5をexpInfo['eccentricity']に書き換えればよいはずです。
[expInfo['eccentricity'] * cos(deg2rad(targetPos)),
expInfo['eccentricity'] * sin(deg2rad(targetPos))]
同様に、target sizeの値はexpInfo['target size']と書けば取り出せます。この値は [サイズ [w, h] $] の4.0に対応しますから、 [サイズ [w, h] $] を以下のように書き換えます。
[expInfo['target size'], expInfo['target size']]
図5.8 実験情報ダイアログから数値を読み込んでプロパティに設定するとエラーが表示されます。実験情報ダイアログに入力されたものが数値ではなく文字列となっているのが原因です。¶
これで改造は終了のはずなのですが、いざ実験を実行してみると、教示画面が終わってターゲットが提示される直前にエラーで停止してしまいます( 図5.8 下)。英語のエラーメッセージで難しそうですが、一番下の行を読むとcould not convert string to floatと書かれています。stringとは文字列、floatとは浮動小数点数( 表5.1 )のことですから、文字列を浮動小数点数に変換できなかったということです。どういう事かといいますと、例えばeccentricityに4.0と入力されていた場合、Builderには4.0という数値ではなく「4」、「.」、「0」という三文字の文字列に見えているということです。人間としては「数値を入力したいに決まっているだろう、そのぐらい察してくれよ」と言いたくなりますが、Builderはそのような配慮はしてくれません。仕方がないので、明示的にこれは数値として解釈しなさいとBuilderに教えてなければいけません。そのために使用できるのがPythonのデータ型変換関数( 表5.4 )です。float( )関数は、引数に与えられたデータを浮動小数点数に変換して返します。データは整数型のように浮動小数点数ではない数値でも構いませんし、浮動小数点数として解釈できる文字列でも構いません。浮動小数点数として解釈不可能なデータが与えられるとエラーになります。このfloat( )関数を用いると、eccentricityの項目に入力された値を数値に変換することが出来ます。
関数 |
概要 |
|---|---|
int(x) |
xを整数に変換します。xが小数だった場合、小数点以下の値は切り捨てられます。 |
float(x) |
xを浮動小数点数に変換します。 |
str(x) |
xを文字列に変換します。 |
list(x) |
xをリストに変換します。 |
tuple(x) |
xをタプル(12.9.1 節)に変換します |
float(expInfo['eccentricity'])
これを [位置 [x, y] $] の式に当てはめると以下のようになります。長くて読みづらいですが頑張って先ほどエラーとなった式と見比べてください。
[float(expInfo['eccentricity']) * cos(deg2rad(targetPos)),
float(expInfo['eccentricity']) * sin(deg2rad(targetPos))]
同様に、 [サイズ [w, h] $] の式も以下のように訂正しましょう。
[float(expInfo['target size']), float(expInfo['target size'])]
訂正が終わったら実行してください。今度こそ、実験情報ダイアログに入力した値でターゲットの大きさや固視点からの距離を変更できるはずです。
これで改造は完了ですが、実験情報ダイアログについて触れたついでにxlxs記録ファイルへの出力についてひとつ補足しておきます。exp05b.psyexpを実行して出来たxlsx記録ファイルを見ると、ワークシートの最後に 図5.9 のように実験情報ダイアログに入力した値が記録されているのがわかります。分析の際に役に立つことも多いので覚えておいてください。
あと、本章で入力した式はとても長くてプロパティ設定ダイアログの入力欄に入りきらず、とても編集しづらかったのではないかと思います。この問題は 第6章 で取り上げるCodeコンポーネントを使用するとある程度改善されます。詳しくは「 6.10.6:Codeコンポーネントを使ってプロパティ設定ダイアログに複雑な式を直接入力しないようにする 」をご覧ください。
- チェックリスト
実験情報ダイアログに入力されたデータの型を答えることが出来る。
データを整数型、浮動小数点型、文字列型、リストに変換することが出来る。
実験情報ダイアログを用いて刺激の大きさや位置などの値を実験開始時に指定するように実験を作ることが出来る。
図5.9 xlsx記録ファイルを開くと、ワークシートの最後に実験情報ダイアログに入力された値が記録されています。¶
5.6. 練習問題：パラメータが適切な範囲を超えないようにしよう¶
この章ではBuilderのPythonのコードを書いてみました。まだまだ解説したいことはたくさんありますが、ここで一区切りとします。最後に練習問題として、exp05a.psyexpを改造して、trialルーチンでキーが押されるまで刺激を提示し続けるようにしてください。ターゲット出現後6秒以上経過した後はキーが押されるまで、targetStimの [色] はずっと$[1.0, 1.0, 1.0]の値を保ち続けるものとします。
キーが押されるまでtrialルーチンを継続し、刺激を提示し続けることはこの章まで進んだ皆さんなら問題はないはずです。この問題のポイントは、exp05a.psyexpにおいて、trialルーチンが6秒以上継続してしまうとtargetStimの [色] に入力した式($[t/6.0, t/6.0, t/6.0])の値が1.0を超えてしまう点です。一度皆さんも試してみていただければと思いますが、 [色] に入力した式をexp05a.psyexpのまま変更せずに6秒以上刺激を提示すると、モノクロのグレーティング刺激を提示していたはずなのに突然カラーグレーティングが提示されてしまいます。そのまま放置していると実験が正常に動作しなくなる場合もありますので、現象を確認したらすぐにエスケープキーを押して実験を終了しましょう。 [色] に入力した式のRGB各成分の値が1.0を超えないようにする方法を考えてください。練習ついでに、targetStimの [位相 (周期に対する比) $] の式を t にして「フレーム毎に更新する」にしてみましょう。グレーティング刺激を運動させることが出来ます。運動知覚の実験ではよく使われる刺激ですので覚えておく価値があると思います。
どうしても答えがわからないという方向けに少しだけヒント。 表5.2 のいずれかの関数を使えば式の値が一定値を超えないように制限することが出来ます。
5.7. この章のトピックス¶
5.7.1. 他の数学関数を使用する方法¶
本文中で述べたとおり、指数関数e^xは標準の状態ではBuilderに読み込まれません。Pythonの膨大な数学関数を利用するためには、第6章 で紹介するCodeコンポーネントを用いてそれらの関数をBuilderに読み込む必要があります。詳しくは 第6章 を参照していただきたいのですが、Codeコンポーネントを用いて実験の最初に以下のコードを実行すると、exp(x)というxの指数関数の値を得る関数が利用できるようになります。
from numpy import exp
一般に、fooというパッケージ（またはモジュール）に含まれるbarという名前の関数等を参照する時には
from foo import bar
と書きます。Codeコンポーネントを用いて読み込んだ場合は使用済み名前のチェックが効かないので十分に注意してください。もっと踏み込んだ話をしますと、異なるパッケージで同一の名前の関数が存在する場合がありますので、上記のfromを用いる方法よりも
import foo
と書いてfooパッケージを読み込み、
foo.bar(x)
という具合にドット演算子を使ってパッケージ名を明示する方が安全です。
5.7.2. Python2における整数同士の割り算とBuilderにおける扱い(上級)¶
本書はPython3ベースのPsychoPyを想定していますが、Python2ベースのPsychoPyを使用する人は整数同士の割り算の扱いに注意する必要があります。というのも、 Python2では整数同士の割り算の結果は整数となる からです。例えば、4 / 3の値は1.3333333ではなく1となります。四捨五入ではなく切り捨てが行われるので、5 / 3の値も1となります。どちらか一方が小数であれば結果も小数となるので、4.0 / 3 は1.3333333、 5 / 3.0 = 1.6666667となります。Python3では整数同士の割り算でも割り切れない場合は小数の結果が得られます。「現在なんらかの必要があってPython2を使用しているけれども、将来的にはPython3への移行を考えている」という人は注意してください。
なお、Python2.6から導入された __future__ パッケージのdivisionをimportすることにより、Python2でも整数同士の割り算がPython3と同じ挙動になります。バージョン1.73.04以降のPsychoPy Builderでは自動的にdivisionがimportされるため、Python2ベースのPsychoPy Builderでも整数同士の割り算についてはPython3と同様の動作となります。
5.7.3. Python2とPython3の文字列の違い(上級)¶
「3.11.6:$を含む文字列を提示する 」でも触れたように、コンピュータでは文字に数値を割り振ることによって文字を管理しています。地域によって使用される文字コードが異なるため、ある文字コードで書かれた文書を別の文字コードを使用するコンピュータで閲覧すると本来とは異なる文字で表示されてしまうという問題が生じます。この問題を解消するために、世界各地のコンピュータで使用されている文字を網羅する共通の文字コードを制定しようとしたのがUnicodeです。Unicodeを利用することによって、従来は異なる文字コードで表現されていた複数の言語を同一の文書に混在させることが簡単になりました。Unicodeですべての問題が解決したわけではないのですが、英語圏で開発されているPsychoPyで問題なく日本語の文章を刺激として提示できるのはUnicodeのおかげです。
このように非常にありがたいUnicodeですが、実際に皆さんが使っているPCのオペレーティングシステム(OS)自体はそれぞれの文字コードで動作しているので、どうしても両者をうまく使い分ける必要があります。そして困ったことに、この使い分け方がPython2と3の間で異なるのです。 図5.10 をご覧ください。Python2、3ともに基本の文字列型はstr型ですが、str型はPython2ではOSの文字コード、Python3ではUnicodeが使われます。そして、Python2でUnicode文字列を使う時はunicode型の文字列オブジェクトを使用する必要があります。逆にPython3でPython2のstr型に相当するものが必要な時はbyte型というタイプのオブジェクトを使用します。
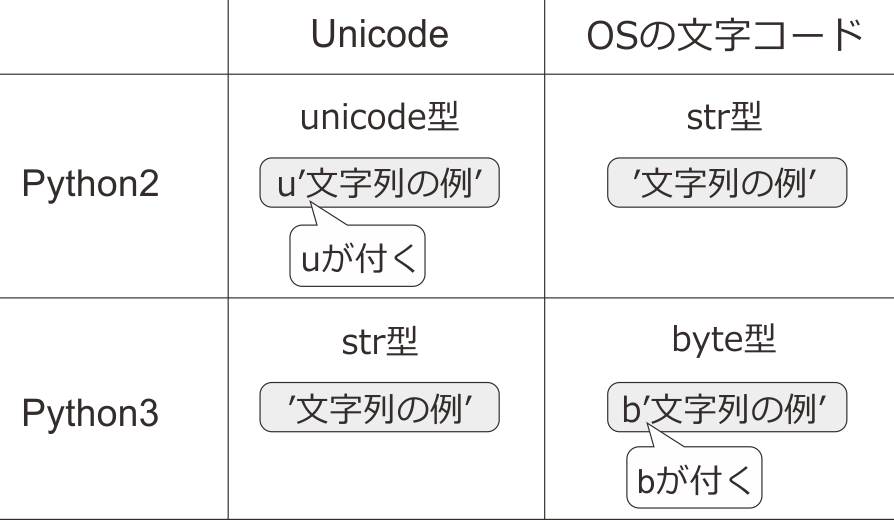
図5.10 Python2と3の文字列型と文字コード¶
Python3を使っている場合、少なくとも本書で想定しているレベルの用途ではbyte型を使うことはまずありません。したがって、文字列はstr型でUnicodeを使用していると考えて良いです。しかし、Python2を使っている場合は、基本がUnicode型ではないので、日本語を使う時には明示的にunicode型のオブジェクトを使用する必要があります。具体的には、文字列を記述する際には u'文字列の例' のようにシングルクォーテーションまたはダブルクォーテーションの前に u を付ける必要があります。もし本書の読者で使用機材の都合などでPython2を使用している方がおられたら、本書の解説を読む際に日本語や全角記号などを含む文字列の前にはすべて u が付いているつもりで読んでください。幸い、 u が不要な文字列に u を付けてもエラーにはなりませんので、迷ったときはとりあえず u を付けると良いでしょう。